最短路入门

Dijkstra 算法

1. 定义概览

Dijkstra（迪杰斯特拉）算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra 算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

2. 算法描述

1) 算法思想：

设 G=(V,E) 是一个带权有向图，把图中顶点集合 V 分成两组，第一组为已求出最短路径的顶点集合（用 S 表示，初始时 S 中只有一个源点，以后每求得一条最短路径 , 就将加入到集合 S 中，直到全部顶点都加入到 S 中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用 U 表示），按最短路径长度的递增次序依次把第二组的顶点加入 S 中。在加入的过程中，总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S 中的顶点的距离就是从 v 到此顶点的最短路径长度，U 中的顶点的距离，是从 v 到此顶点只包括 S 中的顶点为中间顶点的当前最短路径长度。

2) 算法步骤：

a. 初始时，S 只包含源点，即 S ＝{v}，v 的距离为 0。U 包含除 v 外的其他顶点，即：U={其余顶点}，若 v 与 U 中顶点 u 有边，则<u,v>正常有权值，若 u 不是 v 的出边邻接点，则<u,v>权值为 ∞。

b. 从 U 中选取一个距离 v 最小的顶点 k，把 k，加入 S 中（该选定的距离就是 v 到 k 的最短路径长度）。

c. 以 k 为新考虑的中间点，修改 U 中各顶点的距离；若从源点 v 到顶点 u 的距离（经过顶点 k）比原来距离（不经过顶点 k）短，则修改顶点 u 的距离值，修改后的距离值的顶点 k 的距离加上边上的权。

d. 重复步骤 b 和 c 直到所有顶点都包含在 S 中。

执行动画过程如下图

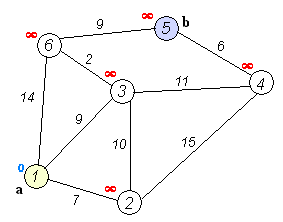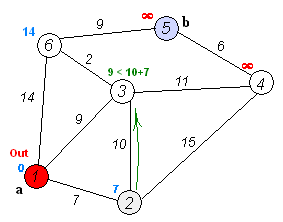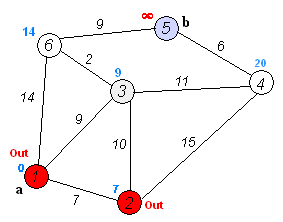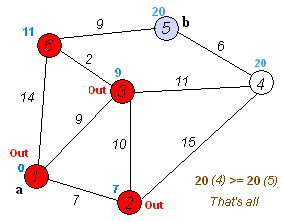
spfa 算法

spfa 是一种求单源最短路的算法

算法中需要用到的主要变量

int n; //表示 n 个点，从 1 到 n 标号

int s,t; //s 为源点，t 为终点

int d[N]; //d[i] 表示源点 s 到点 i 的最短路

int p[N]; //记录路径（或者说记录前驱）

queue q; //一个队列，用 STL 实现，当然可有手打队列，无所谓

bool vis[N]; //vis[i]=1 表示点 i 在队列中 vis[i]=0 表示不在队列中

几乎所有的最短路算法其步骤都可以分为两步

1. 初始化

2. 松弛操作

初始化：

d 数组全部赋值为 INF（无穷大）；p 数组全部赋值为 s（即源点），或者赋值为-1，表示还没有知道前驱，然后 d[s]=0; 表示源点不用求最短路径，或者说最短路就是 0。将源点入队； （另外记住在整个算法中有顶点入队了要记得标记 vis 数组，有顶点出队了记得消除那个标记）

队列+松弛操作

读取队头顶点 u，并将队头顶点 u 出队（记得消除标记）；将与点 u 相连的所有点 v 进行松弛操作，如果能更新估计值（即令 d[v] 变小），那么就更新，另外，如果点 v 没有在队列中，那么要将点 v 入队（记得标记），如果已经在队列中了，那么就不用入队

以此循环，直到队空为止就完成了单源最短路的求解

SPFA 可以处理负权边

定理：只要最短路径存在，上述 SPFA 算法必定能求出最小值。

证明：
　　每次将点放入队尾，都是经过松弛操作达到的。换言之，每次的优化将会有某个点 v 的最短路径估计值 d[v] 变小。所以算法的执行会使 d 越来越小。由于我们假定图中不存在负权回路，所以每个结点都有最短路径值。因此，算法不会无限执行下去，随着 d 值的逐渐变小，直到到达最短路径值时，算法结束，这时的最短路径估计值就是对应结点的最短路径值。（证毕）

期望的时间复杂度 O(ke)， 其中 k 为所有顶点进队的平均次数，可以证明 k 一般小于等于 2。

判断有无负环：
　　如果某个点进入队列的次数超过 N 次则存在负环（SPFA 无法处理带负环的图）

代码