Wannafly 挑战赛 18-序列

2018-07-18 2018-07-18 约 482 字预计阅读 1 分钟 - 次阅读

警告

本文最后更新于 2018-07-18，文中内容可能已过时。

时间限制：C/C++ 1 秒，其他语言 2 秒
空间限制：C/C++ 262144K，其他语言 524288K
64bit IO Format: %lld

题目描述

有一个长度为 n 的序列 a，已知 a[1]=a[n]=1，且对于 2 <= x <= n，a[x] / a[x-1] 是以下三个数字之一 [ 1，-2，0.5 ], 问有多少种不同的序列满足题意。
两个序列不同当且仅当它们有至少一个位置上的数字不同，序列 a 可以为任何实数。

输入描述：

一个整数表示 n (1<= n <= 1e3)

输出描述：

一个整数表示答案模 109+7

示例 1

输入

5 输出

7

解题思路：
整体来看，a[x] = a[x-1] _ [1, -2, 0.5]，那么等于从 n-1 个 [1,-2,0.5] 中选出 n-1 个数值相乘（a[x-1]=a[x-2] _ [1,-2,0.5] 同理化简式子），
最后答案要是 1，所以-2 就必须有偶数个，同理 0.5 的个数要等于-2. 顺序无关。那所有的转换中，就只要保证有若干组 (-2,-2,0.5,0.5) 存在

表示偶数个 2 的个数与偶数个 0.5 的个数组合；组合数用二项式系数，杨辉三角来求。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e3 + 5;
const int mod = 1e9 + 7;
long long c[maxn][maxn];

int main(){
    for(int i = 0; i < maxn; i++){//杨辉三角
        c[i][0] = 1;
        c[i][i] = 1;
        for(int j = 1; j < i; j++)
            c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod;
    }
    int n;
    while(~scanf("%d", &n)){
        n--;
        long long ans = 0;
        for(int i = 0; i*2 <= n; i += 2){
            ans = (ans%mod + (c[n][i]*c[n-i][i])%mod)%mod;
        }
        printf("%lld\n", ans);
    }
    return 0;
}

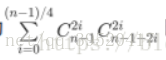
Buy me a coffee~

赞赏

支付宝

微信