Index

Jian YE 收录于 DL

2024-04-26 2024-05-05 约 8493 字预计阅读 17 分钟 - 次阅读

1、⭐softmax如何防止指数上溢

原softmax公式：

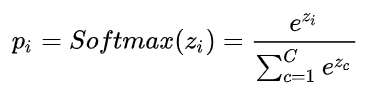
工程化实现，防止指数上溢：

，使a等于x中最大值。

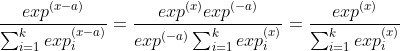
2、⭐Transformer中的positional encoding

为什么需要PE: 因为transfomer是同时处理所有输入的，失去了位置信息。
编码应该满足的条件：a、对于每个位置词语，编码是唯一的 b、词语之间的间隔对于不同长度句子是一致的 c、能适应任意长度句子
公式：每个词语位置编码为不同频率的余弦函数，从1到1/10000。如下将每个词语位置编码为d维向量–>

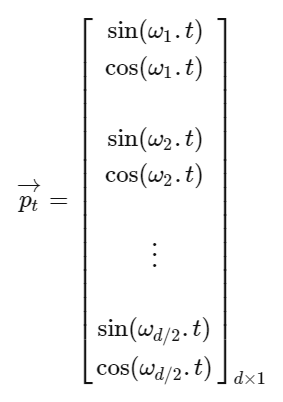
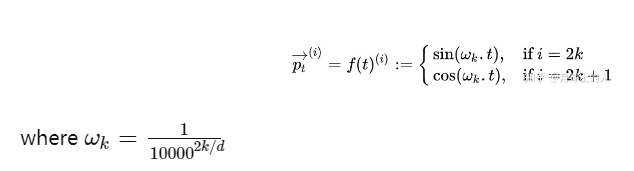
可理解为一种二进制编码，二进制的不同位变化频率不一样，PE的不同位置变化频率也不一样

如何获取相对位置关系：两个位置编码进行点积。

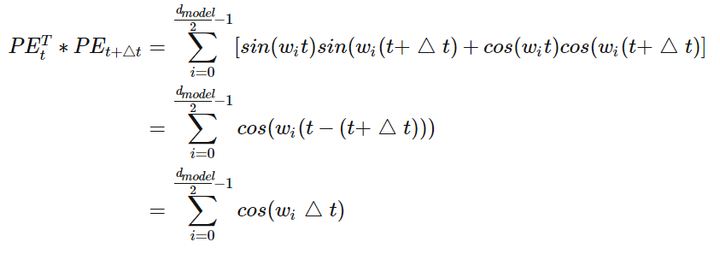
3、⭐求似然函数步骤

定义：概率是给定参数，求某个事件发生概率；似然则是给定已发生的事件，估计参数。

写出似然函数
对似然函数取对数并整理
求导数，导数为0处为最佳参数
解似然方程

4、⭐HMM和CRF区别

CRF是判别模型，对问题的条件概率分布建模；HMM是生成模型，对联合概率分布建模
HMM是概率有向图，CRF是概率无向图
HMM求解过程可能是局部最优，CRF是全局最优

5、⭐空洞卷积实现

相比于常规卷积多了dilation rate超参数，例如dilation rate=2代表相邻两个卷积点距离为2，如图(b)。

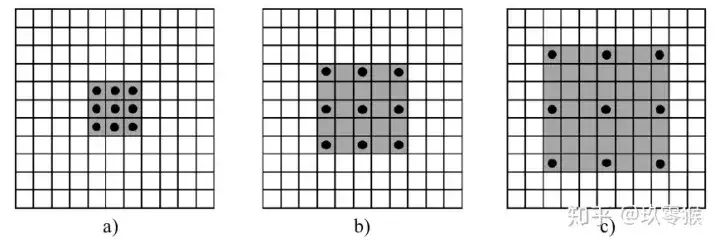
存在问题：gridding effect, 由于卷积的像素本质上是采样得到的，所以图像的局部相关性丢失了，同时远距离卷积得到的信息也没有相关性。

6、⭐汉明距离

两个字符串对应位置的不同字符的个数。

7、⭐训练过程中发现loss快速增大应该从哪些方面考虑?

学习率过大
训练样本中有坏数据

8、⭐Pytorch和TensorFlow区别

图生成：pytorch动态图，tensorflow静态图
设备管理：pytorch cuda，tensorflow 自动化

9、⭐model.eval vs和torch.no_grad区别

model.eval: 依然计算梯度，但是不反传；dropout层保留概率为1；batchnorm层使用全局的mean和var
with torch.no_grad: 不计算梯度

10、⭐每个卷积层的FLOPS计算

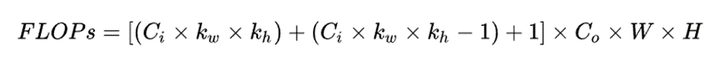
即计算feature map每个点需要的乘法和加法运算量，定义一个乘法和加法为一次flop，则FLOPS计算如下：

11、⭐PCA(主成分分析)

⭐PCA是一种降维方法，用数据里面最主要的方面来代替原始数据，例如将$m$个$n$维数据降维到$n’$维，希望这$m$个$n’$维数据尽可能地代表原数据。
⭐两个原则：最近重构性–>样本点到这个超平面的距离足够近；最大可分性–>样本点在这个超平面的投影尽可能的分开。
⭐流程：基于特征值分解协方差矩阵和基于奇异值分解SVD分解协方差矩阵。

（1）对所有样本进行中心化

（2）计算样本的协方差矩阵$XX^T$

（3）对协方差矩阵进行特征值分解

（4）取出最大的$n’$个特征值对应的特征向量，将所有特征向量标准化，组成特征向量矩阵W

（5）对样本集中的每一个样本$x^(i)$转化为新的样本$z^(i)=W^T x^(i)$，即将每个原数据样本投影到特征向量组成的空间上

（6）得到输出的样本集$z^(1)、z^(2)…$

⭐意义：a、使得结果容易理解 b、数据降维，降低算法计算开销 c、去除噪声

12、⭐k-means如何改进？

⭐缺点：1、k个初始化的质心对最后的聚类效果有很大影响 2、对离群点和孤立点敏感 3、K值人为设定
⭐改进：
- K-means++：从数据集随机选择一个点作为第一个聚类中心，对于数据集中每一个点计算和该中心的距离，选择下一个聚类中心，优先选择和上一个聚类中心距离较大的点。重复上述过程，得到k个聚类中心。
- K-medoids：计算质心时，质心一定是某个样本值的点。距离度量：每个样本和所有其他样本的曼哈顿距离$((x,y), |x|+|y|)$。
- ISODATA，又称为迭代自组织数据分析法，是为了解决K值需要人为设定的问题。核心思想：当属于某个类别的样本数过少时或者类别之间靠得非常近就将该类别去除；当属于某个类别的样本数过多时，把这个类别分为两个子类别。
⭐和分类问题的区别：分类的类别已知，且需要监督；k-means是聚类问题，类别未知，不需要监督。
⭐终止条件：a、相邻两轮迭代过程中，非质心点所属簇发生改变的比例小于某个阈值 b、所有簇的质心均未改变 c、达到最大迭代次数
⭐时间复杂度：$O(迭代次数 \ast 数据个数 \ast k \ast 数据维度)$，k为k个类别中心
⭐空间复杂度：$O(数据个数 \ast 数据维度+k \ast 数据维度)$

13、⭐Dropout实现

以p的概率使神经元失效，即使其激活函数输出值为0：

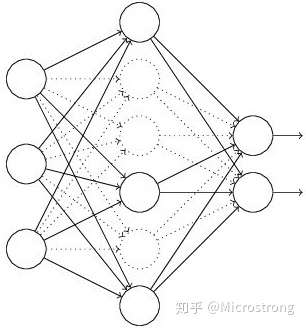
为了使训练和测试阶段输出值期望相同，需要在训练时将输出值乘以1/(1-p)或者在测试时将权重值乘以(1-p)。

Dropout和Batch norm能否一起使用？

可以，但是只能将Dropout放在Batch norm之后使用。因为Dropout训练时会改变输入X的方差，从而影响Batch norm训练过程中统计的滑动方差值；而测试时没有Dropout，输入X的方差和训练时不一致，这就导致Batch norm测试时期望的方差和训练时统计的有偏差。

14、⭐梯度消失和梯度爆炸

梯度消失的原因和解决办法

（1）隐藏层的层数过多

反向传播求梯度时的链式求导法则，某部分梯度小于1，则多层连乘后出现梯度消失

（2）采用了不合适的激活函数

如sigmoid函数的最大梯度为1/4，这意味着隐藏层每一层的梯度均小于1（权值小于1时），出现梯度消失。

解决方法：1、relu激活函数，使导数衡为1 2、batch norm 3、残差结构

梯度爆炸的原因和解决办法

（1）隐藏层的层数过多，某部分梯度大于1，则多层连乘后，梯度呈指数增长，产生梯度爆炸。

（2）权重初始值太大，求导时会乘上权重

解决方法：1、梯度裁剪 2、权重L1/L2正则化 3、残差结构 4、batch norm

15、⭐YOLOV1-YOLOV4改进

⭐YOLOV1:

one-stage开山之作，将图像分成S*S的单元格，根据物体中心是否落入某个单元格来决定哪个单元格来负责预测该物体，每个单元格预测两个框的坐标、存在物体的概率（和gt的IoU）、各类别条件概率。
损失函数：均采用均方误差。
优点：速度快。
缺点：1、每个单元格预测两个框，并且只取和gt IoU最大的框，相当于每个单元格只能预测一个物体，无法处理密集物体场景。2、输出层为全连接层，只能输入固定分辨率图片 3、计算IoU损失时，将大小物体同等对待，但同样的小误差，对大物体来说是微不足道的，而对小物体来说是很严重的，这会导致定位不准的问题。4、没有密集锚框、没有RPN，导致召回率低

⭐YOLOV2:

改进点：

(1)、Batch normalization替代dropout，防止过拟合

(2)、去掉全连接层，使用类似RPN的全卷积层

(3)、引入Anchor，并使用k-means聚类确定anchor大小、比例，提高了recall

(4)、高分辨率预训练backbone

(5)、限定预测框的中心点只能在cell内，具体通过预测相对于cell左上角点的偏移实现，这样网络收敛更稳定

(6)、添加passthrough层，相当于多尺度特征融合，$1 \ast 1$卷积将$26 \ast 26 \ast 512$ feature map降维成$26 \ast 26 \ast 64$, 然后将特征重组，拆分为4份$13 \ast 13 \ast 64$，concate得到$13 \ast 13 \ast 256$ feature map，和低分辨率的$13 \ast 13 \ast 1024$ feature map进行concate

(7)、提出Darknet进行特征提取，参数更少，速度更快

(8)、提出YOLO9000，建立层级分类的World Tree结构，可以进行细粒度分类

⭐YOLOV3:

(1)、使用sigmoid分类器替代softmax分类器，可以处理多标签分类问题

(2)、引入残差结构，进一步加深网络深度

(3)、多尺度预测，每个尺度预测3个bbox

⭐YOLOV4:

(1)、Mosaic data augmentation：四张图片拼接成一张图片

(2)、DropBlock：drop out只丢弃单个像素，而因为二维图像中相邻特征强相关，所以丢弃后网络依然可以推断出丢失区域信息，导致过拟合；所以dropblock选择丢弃一块连续区域。

(3)、label smoothing

(4)、CIoU loss CIoU = IoU + bbox中心距离/对角线距离+长宽比例之差

-1<=CIoU<=1

(5)、YOLO with SPP：就是用不同大小的卷积核对特征图进行卷积，得到不同感受野的特征，然后concate到一起。

16、⭐AP计算

⭐AP是对每一类先计算AP，再将所有类平均得到最终AP。以COCO中AP计算为例。先选定用来判断TP和FP的IoU阈值，如0.5，则代表计算的是AP0.5，然后对每类做计算，例如对于class1:

	class1
box1	score1
box2	score2
box3	score3

若box1与某gt的IoU大于指定阈值（如0.5)，记为Positive；若有多个bbox与gt的IoU大于指定阈值，选择其中score最大的记为Positive，其它记为Negative。可理解为确定box1对应的label。box2、box3同理。

而后要得到PR曲线，需要先对box1,2,3按score从高到低排序，假设排序结果如下：

	True class	class1
box2	Positive	score2
box1	Negative	score1
box3	Positive	score3

然后逐行计算score阈值为score2、score1、score3的Precision和Recall，score大于阈值的box才算做模型预测的Positive（TP+FP)。假设共有三个gt box，则计算结果如下：

	True class	class1	Precision=TP/(TP+FP)	Recall
box2	Positive	score2	1/1	1/3
box1	Negative	score1	1/2	1/3
box3	Positive	score3	2/3	2/3

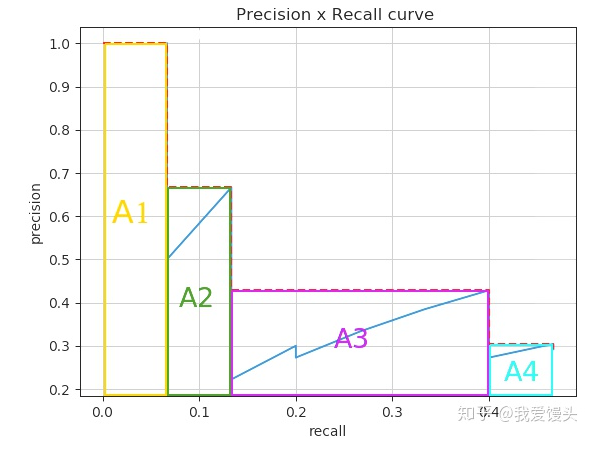
这样得到一个个PR曲线上的点，然后利用插值法计算PR曲线的面积，得到class1的AP。具体插值方法：COCO中是均匀取101个recall值即0,0.01,0.02,…,1，对于每个recall值r，precision值取所有recall>=r中的最大值$p_{interp(r)}$。

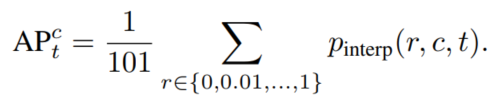
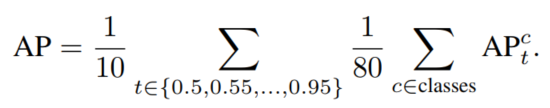
然后每个recall值区间（0-0.01，0.01-0.02，…）都对应一个矩形，将所有矩形面积加起来即为PR曲线面积，得到一个类别的AP，如下图所示。对所有类别（如COCO中80类）、所有IoU阈值（例如0.5:0.95）的AP取均值即得到最终AP。

AR计算 计算过程同AP，也是在所有IoU阈值和类别上平均。每给定一个IoU阈值和类别，得到一个P_R曲线，当P不为0时最大的Recall作为当前Recall。

17、⭐IoU变种合集

IoU

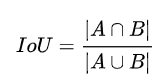
GIoU

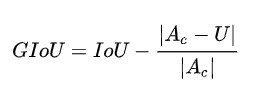
$Ac$为bbox A和bbox B的最小凸集面积，U为A U B的面积，即第二项为不属于A和B的区域占最小闭包的比例。 -1<=GIoU<=1，当A和B不重合，仍可以计算损失，因此可作为损失函数。

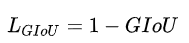
✒️优点：在不重叠的情况下，能让预测框向gt框接近。

✒️缺点：遇到A框被B框包含的情况下，GIoU相同。

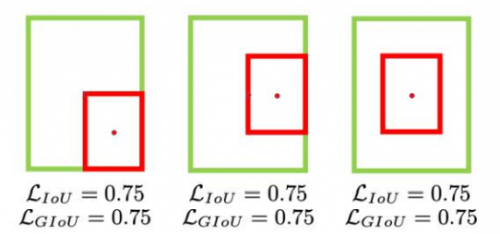
DIoU

其中， $b$和$b^{gt}$分别代表了预测框和真实框的中心点，且$ρ$代表的是计算两个中心点间的欧式距离。$c$代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。

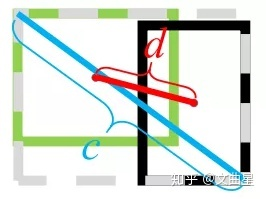
$-1 < DIoU \leq 1$, 将目标与anchor之间的距离，重叠率以及尺度都考虑进去，使得目标框回归变得更加稳定

✒️优点：直接优化距离，解决GIoU包含情况。

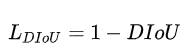
CIoU

在DIoU的基础上考虑bbox的长宽比：

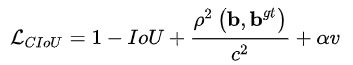
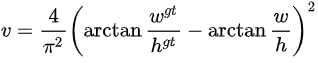
$-1 \leq CIoU \leq 1$

✒️优点：考虑bbox长宽比

18、⭐depth-wise separable conv (深度可分离卷积)

例如$5 \ast 5 \ast 3$图片要编码为$5 \ast 5 \ast 4$ feature map，则depth-wise conv分为两步：先是depth wise卷积，利用3个$3 \ast 3$ conv对每个通道单独进行卷积，这一步只能改变feature map长宽，不能改变通道数：

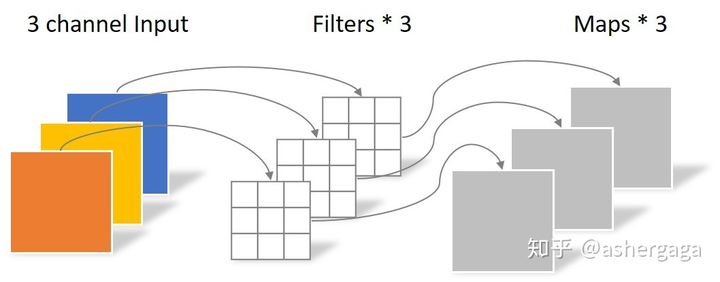
参数量：

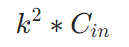
计算量：

然后是point wise卷积，利用4个$1 \ast 1 \ast 3$ conv对depth wise生成的feature map进行卷积，这一步只能改变通道数，不能改变feature map长宽：

参数量：

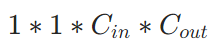
计算量：

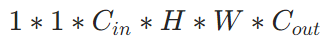
所以与一般卷积对比，总参数量和计算量：

总参数量：常规卷积–>

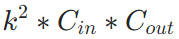
，深度可分离卷积–>

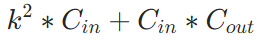
总计算量：常规卷积–>

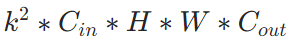
, 深度可分离卷积–>

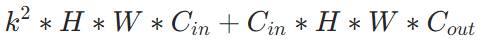
19、⭐检测模型里为啥用smoothL1去回归bbox

首先，对于L2 loss，其导数包含了(f(x)-Y)，所以当预测值与gt差异过大时，容易梯度爆炸；而对于L1 loss，即使训练后期预测值和gt差异较小，梯度依然为常数，损失函数将在稳定值附近波动，难以收敛到更高精度。

所以SmoothL1 loss结合了两者的优势，当预测值和gt差异较大时使用L1 loss；差异较小时使用L2 loss：

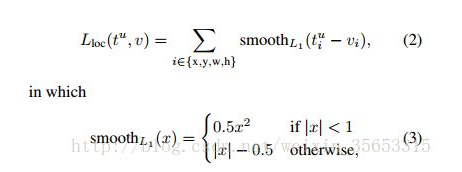
20、⭐Deformable conv如何实现梯度可微？

指的是对offset可微，因为offset后卷积核所在位置可能是小数，即不在feature map整数点上，所以无法求导；Deformable conv通过双线性插值实现了offset梯度可微。用如下表达式表达常规CNN:

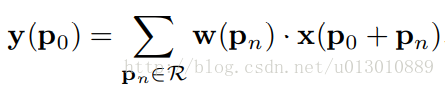
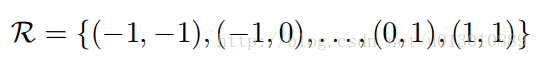
则Deformable conv可表达为：

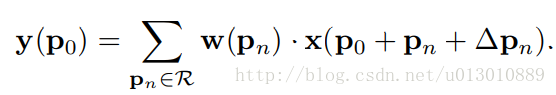
$x(p_0+p_n+\Delta p_n)$可能不是整数，需要进行插值，任意点p（周围四个整数点为q）的双线性插值可表达为下式：

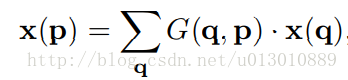
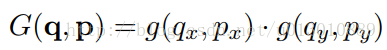
其中$g(a, b) = max(0, 1 − |a − b|)$。

则offest delta_pn求导公式为：

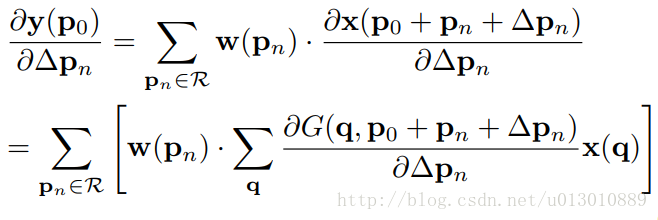
从而实现对offset的梯度可微。

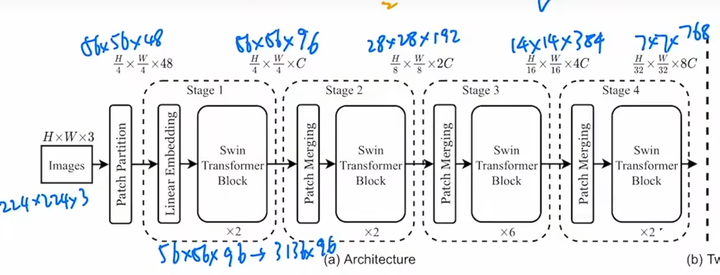
21、⭐Swin Transformer

(1)⭐motivation 高分辨率图像作为序列输入计算量过大问题；和nlp不同，cv里每个物体的尺度不同，而nlp里每个物体的单词长度都差不多。

(2)⭐idea 问题一：一张图分成多个窗口，每个窗口分成多个patch，每个窗口内的多个patch相互计算自注意力；问题二：模仿CNN pooling操作，将浅层尺度patch进行path merging得到一个小的patch，实现降采样，从而得到多尺度特征。

(3)⭐method 整体结构很像CNN，卷积被窗口自注意力代替，pooling被patch merging代替。

✒️method 1: shifted window

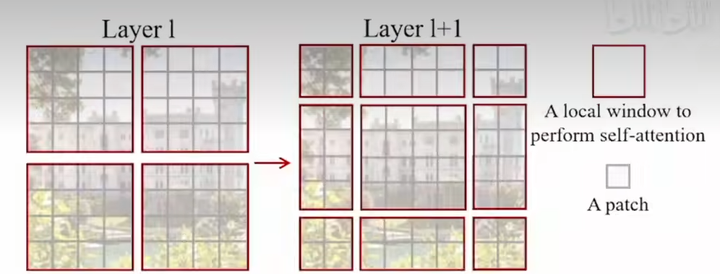
目的是让不重叠窗口区域也能有交互，操作本质是将所有窗口往右下角移动2个patch。

窗口数从4个变成了9个，计算量增大，为减小计算量，使用cyclic shift，将窗口拼接成4个窗口，另外因为拼接后A、B、C相较于原图发生了相对位置变化，所以A、B、C和其他区域是不可以进行交互的，因此引入了Mask操作。

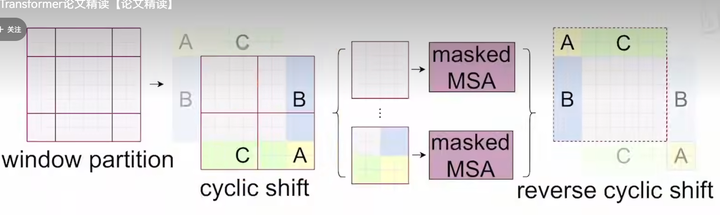
Mask操作：

以3、6所在窗口的自注意力计算为例，将7*7=49个像素展平得到长度为49的一维向量，做矩阵乘法即Q*K。

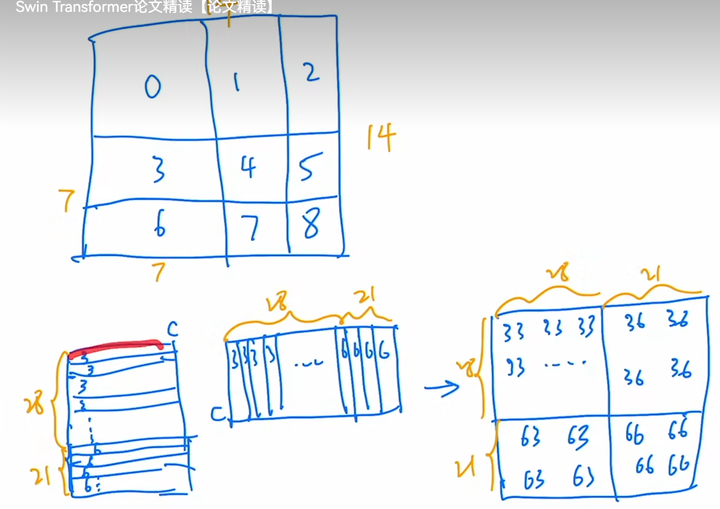
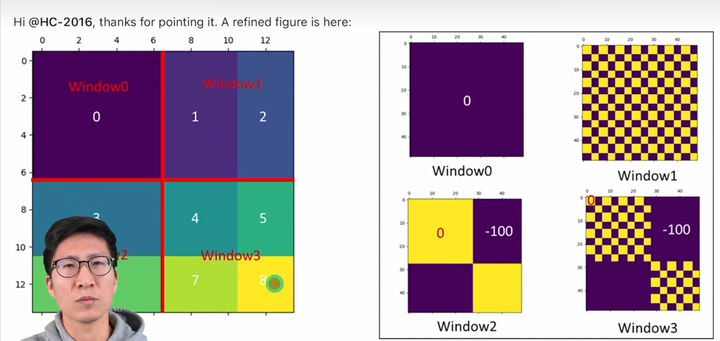
又因为3和6是不可以交互的，所以矩阵左下角和右上角应该被mask掉，Swin采用的方法是加上左下角和右上角为-100，其余位置为0的模板，这样得到的attention矩阵在softmax后就变成0了。

✒️method2: patch merging 就是间隔采样，然后在通道维度上拼接

(4)⭐SwinTransformer位置编码实现

👉核心思想就是建了一个相对位置编码embedding字典，使得相同的相对位置编码成相同的embedding。👈

例如2*2的patch之间的相对位置关系矩阵为2*2*2，相对位置范围为[-1,1]：

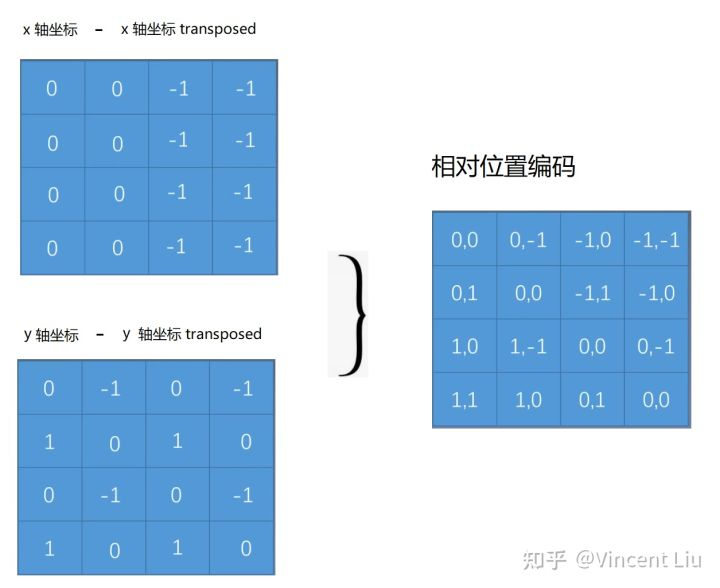
则x，y相对位置关系可用3*3 (-1,0,1三种相对位置)的table存储所有可能的相对位置关系，并用3*3*embed_n表示所有相对位置对应的embedding。为了使得索引为整数，需要将所有相对位置变为正值：

可以通过简单的x,y相对位置相加将相对位置映射为一维，但是会出现(0,2)和(2,0)无法区分的问题，所以需要使得x,y相对位置编码不同：

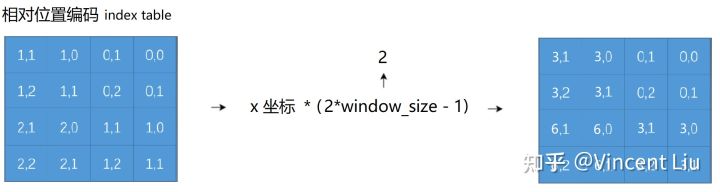
然后将x和y相对位置相加：

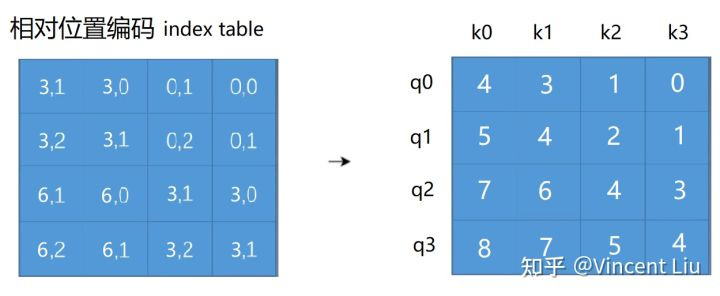
从而每个相对位置对应一个一维的值，作为相对位置embedding table的索引，获取对应位置的embedding。

22、⭐YOLOX核心改进：

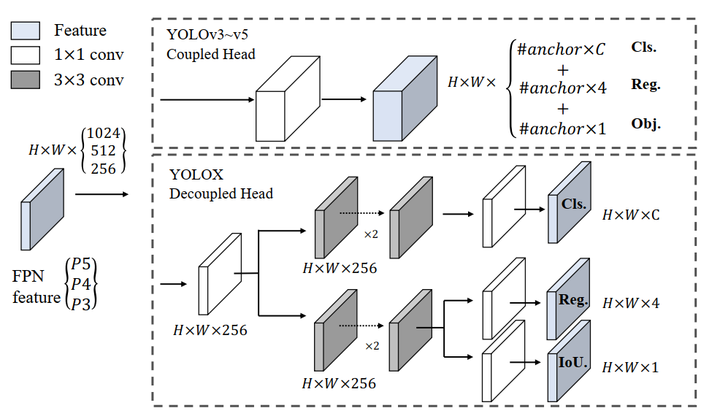
(1)✒️Decoupled head：就是anchor free方法里最常用的cls head和reg head

(2)✒️Anchor-free: 即类似FCOS，不同的是预测的是中心点相对于grid左上角坐标的offset值，以及bbox的长宽，将物体中心的某个区域内的点定义为正样本，并且每个尺度预测不同大小物体。

(3)✒️Label assignment(SimOTA): 将prediction和gt的匹配过程建模为运输问题，使得cost最小。

cost表示：$pred_i$和$gt_j$的cls和reg loss。
对每个gt，选择落在指定中心区域的top-k least cost predictions当作正样本，每个gt的k值不同。
最佳正锚点数量估计：某个gt的适当正锚点数量应该与该gt回归良好的锚点数量正相关，所以对于每个gt，我们根据IoU值选择前q个预测。这些IoU值相加以表示此gt的正锚点估计数量。

23、⭐L1、L2正则化的区别

✒️L1正则化容易得到稀疏解，即稀疏权值矩阵，L2正则化容易得到平滑解（权值很小）。

✒️原因：a、解空间角度：二维情况，L1正则化：||w1||+||w2||，则函数图像为图中方框，显然方框的角点容易是最优解，而这些最优解都在坐标轴上，权值为0.

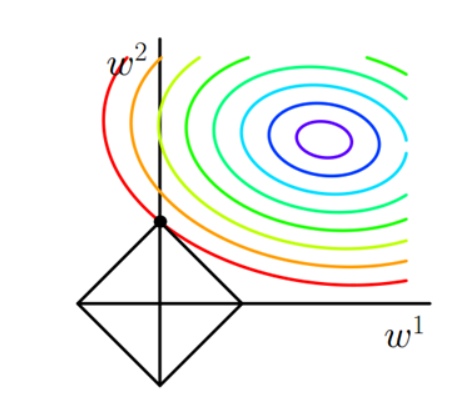
b、梯度下降角度添加正则项 $\lambda \theta^2_j$，则L对$\theta_j$的导数为$2\lambda \theta_j$，梯度更新时$\theta_j=\theta_j-2 \lambda \theta_j=(1-2 \lambda) \theta_j$，相当于每次都会乘以一个小于1的数，使得$\theta_j$越来越小。

24、⭐深度学习花式归一化之Batch/Layer/Instance/Group Normalization

✒️Batch Normalization

⭐核心过程：顾名思义，对一个batch内的数据计算均值和方差，将数据归一化为均值为0、方差为1的正态分布数据，最后用对数据进行缩放和偏移来还原数据本身的分布，如下图所示。

Batch Norm 1d 输入是b*c, 输出是b*c，即在每个维度上进行normalization。
Batch Norm 2d 例如输入是b*c*h*w，则计算normlization时是对每个通道，求bhw内的像素求均值和方差，输出是1*c*1*1。

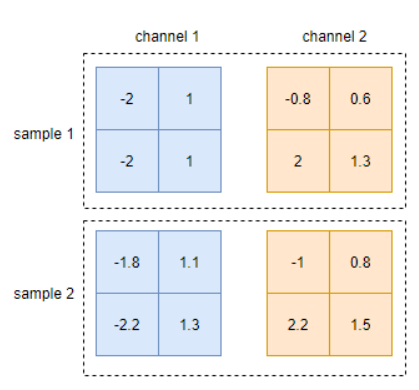
BN测试时和训练时不同，测试时使用的是全局训练数据的滑动平均的均值和方差。
作用：a、防止过拟合 b、加速网络的收敛，internal covariate shift导致上层网络需要不断适应底层网络带来的分布变化 c、缓解梯度爆炸和梯度消失
局限：依赖于batch size，适用于batch size较大的情况

✒️改进：

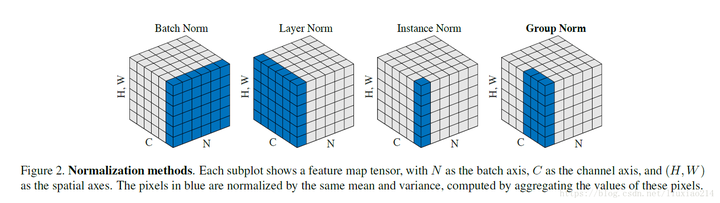
Layer normalization: 对每个样本的所有特征进行归一化，如N*C*H*W，对每个C*H*W进行归一化，得到N个均值和方差。
Instance normalization: 对每个样本的每个通道特征进行归一化，如N*C*H*W，对每个H*W进行归一化，得到N*C个均值和方差。
Group normalization：每个样本按通道分组进行归一化，如N*C*H*W，对每个C*H*W，在C维度上分成g组，则共有N*g个均值和方差。

25、⭐深度学习常用优化器介绍

参考https://zhuanlan.zhihu.com/p/261695487，修正了其中的一些错误。

(1)⭐SGD

a. ✒️公式

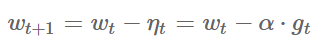
其中$\alpha$是学习率，$g_t$是当前参数的梯度。

b. ✒️优点：每次只用一个样本更新模型参数，训练速度快。

c. ✒️缺点：容易陷入局部最优；沿陡峭方向振荡，而沿平缓维度进展缓慢，难以迅速收敛

(2) ⭐SGD with momentum

a. ✒️公式

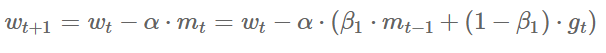
其中$m_t$为动量。

b. ✒️优点：可借助动量跳出局部最优点。

c. ✒️缺点：容易在局部最优点里来回振荡。

(3) ⭐AdaGrad：经常更新的参数已经收敛得比较好了，应该减少对它的关注，即降低其学习率；对于不常更新的参数，模型学习的信息过少，应该增加对它的关注，即增大其学习率。

a. ✒️公式 $$w_{t+1}=w_t-\alpha \cdot g_t / \sqrt{V_t}=w_t-\alpha \cdot g_t / \sqrt{\sum_{\tau=1}^t g_\tau^2}$$ 其中Vt是二阶动量，为累计梯度值的平方和，与参数更新频繁程度成正比。

b. ✒️优点：稀疏数据场景下表现好；自适应调节学习率。

c. ✒️缺点：Vt单调递增，使得学习率单调递减为0，从而使得训练过程过早结束。

(4) ⭐RMSProp：AdaGrad的改进版，不累计所有历史梯度，而是过去一段时间窗口内的历史梯度。

a. ✒️公式 $$\begin{aligned} w_{t+1} & =w_t-\alpha \cdot g_t / \sqrt{V_t} \ & =w_t-\alpha \cdot g_t / \sqrt{\beta_2 \cdot V_{t-1}+\left(1-\beta_2\right) g_t^2}\end{aligned}$$ 即把Vt换成指数移动平均。

b. ✒️优点：避免了二阶动量持续累积、导致训练过程提前结束的问题了。

(5) ⭐Adam：=Adaptive + momentum，即结合了momentum一阶动量+RMSProp二阶动量。

a. ✒️公式 $$\begin{aligned} w_{t+1} & =w_t-\alpha \cdot m_t / \sqrt{V_t} \ & =w_t-\alpha \cdot\left(\beta_1 \cdot m_{t-1}+\left(1-\beta_1\right) \cdot g_t\right) / \sqrt{\beta_2 \cdot V_{t-1}+\left(1-\beta_2\right) g_t^2}\end{aligned}$$

b. ✒️优点：通过一阶动量和二阶动量，有效控制学习率步长和梯度方向，防止梯度的振荡和在鞍点的静止。

c. ✒️缺点：二阶动量是固定历史时间窗口的累积，窗口的变化可能导致Vt振荡，而不是单调变化，从而导致训练后期学习率的振荡，模型不收敛，可通过